Lack of measurement invariance testing is a threat to experimental research

Psychometric instruments are often used in experimental research to infer possible differences in some construct between two or more groups after some manipulations have been administered. Take a random sample of articles from Journal of Experimental Social Psychology, and you might notice a pattern: participants are subjected to an experimental manipulation, after which they give responses, which are averaged to produce sum-scores, which are then compared between the groups to test whether the manipulation had an effect. In this blog post I focus on a particular measurement issue in the context of experimental research: measurement invariance. As far as I’m aware, this topic seems to have received attention mainly in the literature on scale validation and cultural comparisons, and remains undiscussed in experimental research.

The problem of equivalence

Proper functioning of measurement instruments is critical to the line of reasoning described above to ensure that 1) a construct is measured 2) reliably 3) across groups in similar manner. The last one is the assumption of measurement invariance (from here on MI): that an instrument functions equally across different data stratums. In technical terms, model parameters like factor loadings and item intercepts in e.g. confirmatory factor analysis need to have approximately same values for any item across groups. There are several increasingly strict forms of MI. From the least strict to the strictest, the different levels of MI are:

• configural invariance: equivalence of loading patterns across groups
• metric invariance: equivalence of factor loadings across groups
• scalar invariance: equivalence of item intercepts across groups
• residual invariance: equivalence of residual variances across groups

Configural, metric and scalar MIs are important for mean comparisons, residual MI not so much. Testing each of these in latent variable modeling framework involves comparing a series of increasingly constrained CFA models against each other. This can be done with e.g. lavaan and semTools packages of R. For example, testing metric MI is done by comparing a model with factor loadings constrained equal across groups against a model where they are estimated freely. If the constrained model performs significantly worse than unconstrained, this implies differences in the patterns of loadings, and metric MI is considered violated. The same principle holds for scalar and residual MIs as well.

When MI is violated, measurement suffers from a kind of conceptual drift, and in the worst case scenario measures entirely different things, even if the items are exactly same. Here I argue that experimental research has some unique properties that pose a potentially huge threat to MI.

Designed to vary

In situations like the one described in the first paragraph, the intention is to deliberately affect the measurement process, that is, to change mean levels of all items at the same time. However, to prevent violations of MI, those manipulations should NOT affect group covariances, where factorial structures reside.

Often in experimental studies measurements are custom-made to specifically interact with manipulations (or vice versa). I believe this proximity between manipulations and response variables poses a large threat to MI, unique to experimental research, because it might be very difficult to affect the means without altering covariance structures between groups. This might lead to large changes in item intercepts or factor loadings, perhaps some items not loading on a common factor, or even dimensionality assessment suggesting a different number of factors for different groups. In these cases, the meaning of a measurement scale changes between groups, and would result to some extent comparing apples with oranges.

For example, I work in a project where we study perceptions related to actions of robots compared to humans in a moral context. We present hypothetical scenarios where either human or robot agent does something, and ask with Likert-type questions how the agent is perceived. Let’s say this would involve either a human or a robot robbing a bank, and the participants would be randomized to read either human or robot scenario, and we would be interested in moral condemnation between the agents. It can be easily imagined that some items related to morality and punishment can have have entirely different meanings for robots than humans, and relate in different manner to other morality-related items.

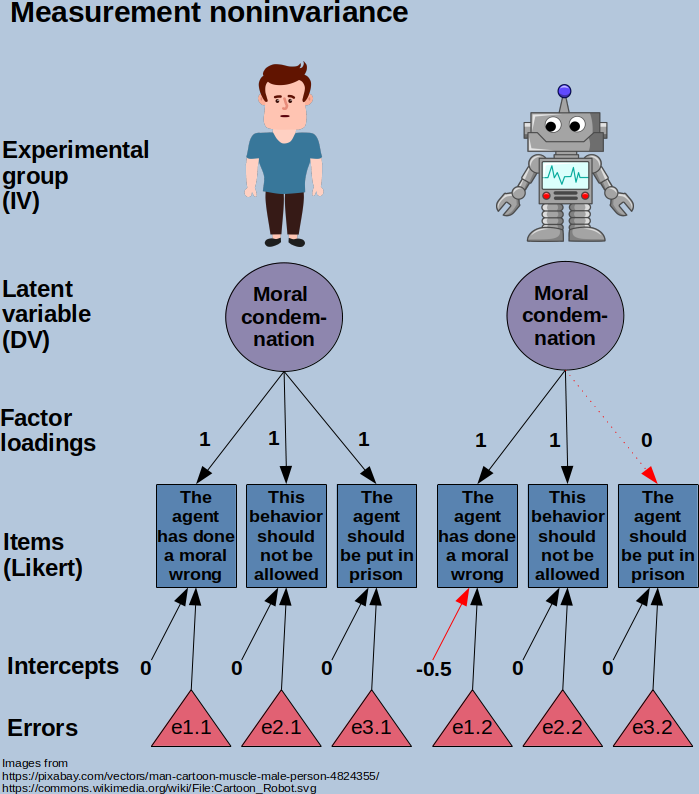
I think this is just too big an issue to be left an assumption, and for this reason believe that MI testing should be considered as a candidate to become standard practice whenever psychometric instruments are used in experimental research. (I’ll openly admit being a hypocrite here. For me, this has been so far limited to some tinkering on my own).

Potential consequences

If the assumption of MI is violated, the consequences can be similar to those we are trying to avoid with other methodological reforms. Steinmetz (2013) has demonstrated that violation of scalar MI (different item intercepts) even by one item can lead to a serious misinterpretation of mean differences between groups: unequal intercepts can both cause spurious differences (increased type 1 error) and attenuate real ones (increased type 2 error). Interestingly, violation of metric invariance (different factor loadings) seems to cause relatively little error. Besides increased error rates, differences in factor structure might imply differences in the meaning of a construct between groups. In the worst case scenario, a ‘measure’ doesn’t even tap into same construct in all groups despite all items being the same.

The current situation

MI tests seem to be virtually non-existent in experimental literature. I personally have never seen an experimental paper report MI tests. Flake, Pek & Hehman (2017) reviewed psychometric information of 39 papers (not necessarily experimental) published in JPSP, and remarked that only one paper mentioned MI. Also, in a recent preprint, Shaw, Cloos, Luong, Elbaz and Flake (2020) examined measurement practices in Many Labs 2 studies, and remarked that adapting stimuli and items for different cultures and/or languages poses a threat to MI. However, to date I have seen no one talk specifically about the possibility that an experimental manipulation itself can pose a threat to MI.

What to do

Use SEM to test for group differences

Personally, I believe moving from sum-score ANOVAs to modeling group differences in latent variable modeling framework could bring forth some big improvements. This has several benefits: the possibility to examine a measurement model and MI, the scores compared use the actual measurement model rather than sums, and SEM has better power to detect group differences. A recent paper gave a nice tutorial how to do this, with syntax for both R and MPLUS (Breitsohl, 2018). Check the supplementary materials for example code.

A potential downside is a likely increased sample size requirement. Every item requires several free parameters, and some common rules of thumb dictate that sample size for SEM should be at least 5-10 subjects per parameter. In some designs this can be higher than what a power analysis would suggest. In this sense, a large number of items is not always a good thing, and additional items very quickly become a burden rather than boon, even if they improve reliability. I have no definitive answer for how to deal this, but think it involving some sort of trade-off between quality and quantity of items.

Report MI tests for DVs

To reiterate, MI testing involves comparing increasingly constrained models against less constrained ones to see whether model fit becomes significantly worse after e.g. intercepts are constrained to be equal across groups. Reporting the strictest level of MI achieved without significantly worsening the model would be a good start. MI assumptions are somewhat notorious for being easily rejected, so categorical rejection might not be the end of the world. For this reason, differences in some key fit indices (like CFI and RMSEA) between subsequent models would also need to be reported to appraise the magnitude of deviation.

However, with the current reporting conventions, I would expect this to feel quite outlandish to some parties making decisions about papers. These analyses would thus likely end up in appendices, supplementary materials or even extra files in external repositories.

Pre-validation of measures?

Well validated measures are always preferred over custom-made scales, but in research situations like described above they might not exist, and I would argue that even if they did, possible violations of MI render prior validation insufficient with novel manipulations. This is because MI is relative to a chosen stratification: no measurement ever in psychology will likely be invariant across all possible stratifications one could make. If measure X is established to be invariant between e.g. men and women, it is still unknown whether it is invariant between young vs. old, low vs. high neuroticism, low vs. high SES, and so on. Because the effect of any novel manipulation (or any other kind of stratification) on group covariances is unknown, MI needs to be established again in these new settings.

This means that demonstrating MI is an inductive problem. Establishing MI in one context cannot guarantee that it holds for any other. Thus it is necessary to demonstrate MI in any situation where a novel manipulation is used with a measure. I believe this is especially the case when indicators and manipulations have a close relationship with each other, and the latter are deliberately crafted to elicit different responses. Prevalidating a measure would thus mean conducting the same study twice. Therefore, prevalidating a measure for these designs is either impossible or redundant. This leaves me to conclude that any study must on its own demonstrate that its measures are invariant across its experimental groups.

Concluding remarks

MI testing seem to be currently non-existent in experimental research leaving us agnostic about the validity of cross-group comparisons. Assumption of MI might hold for any given study, or it might not. We just don’t know. I fear that failure in MI testing in experimental research is a ticking time-bomb similar to persistent power failures of previous decades. Open data can at least allow checking this retrospectively, and whether constraining the measurement models changes the outcomes functions as a kind of sensitivity analysis. It will be up to future research to investigate how common and serious these potential violations are.

Acknowledgements

I want to thank Jukka Sundvall (twitter) for discussions which have advanced these thoughts considerably

References

Breitsohl F. (2018). Beyond ANOVA: An Introduction to Structural Equation Models for Experimental Designs. Organizational Methods Research

Flake J. K., Pek J. & Hehman E. (2017). Construct Validation in Social and Personality Research: Current Practice and Recommendations. Social Psychological and Personality Science

Klein R. A. et al. (2018). Many Labs 2: Investigating Variation in Replicability Across Sample and Setting. Advances in Methods and Practices in Psychological Science

Shaw M., Cloos L., Luong R., Elbaz S., Flake J. K. (2020). Measurement Practices in Large-Scale Replications: Insights from Many Labs 2. PsyArXiv Preprint https://psyarxiv.com/kdurz/

Steinmetz H. (2013). Analyzing observed composite differences across groups: Is partial measurement invariance enough? Methodology: European Journal of Research Methods for the Behavioral and Social Sciences