Ei-merkitsevä p-arvo ei tue ilmiön olemassaolemattomuutta

Aiemmassa kirjoituksessa käsittelin sitä kuinka tilastollisesti merkitsevät ja ei-merkitsevät tulokset eivät automaattisesti ole “ristiriitaisia tuloksia”, ja niiden laskeminen on epätarkka tapa vetää yhteen tutkimusnäyttöä koska tulosten dikotomisointi hävittää informaatiota eikä huomioi tutkimusten laatua. Tässä kirjoituksessa käsittelen laajemmin tilastolliseen merkitsevyyteen liittyvää väärinymmärrystä, joka myös liittyy edellämainittuun: ajatusta että ei-merkitsevä p-arvo tukee nollahypoteesia. Tämä on erittäin yleinen virhekäsitys, ja luultavasti jo muutaman satunnaisen artikkelin poimimalla siihen törmää useita kertoja. Käsittelen myös sitä kuinka hypoteesiä ilmiön olemassaolemattomuudesta voi tukea muuttamalla analyysia hieman.

Hypoteesitestauksen logiikka

Pähkinänkuoressa frekventistisessä tilastotieteessä (kaikki menetelmät joissa lasketaan p-arvoja) asetetaan nollahypoteesi, ja testataan, näyttääkö kerätty data tämän valossa epätodennäköiseltä. Tämä on tyypillisesti muotoiltu: “mitään ei ole meneillään”; kahden ryhmän välillä ei ole eroa tai kahden muuttujan välillä ei ole yhteyttä. Se voi olla esimerkiksi “kissojen ja koirien painoissa ei ole eroa”, tai “älykkyys ja koulusuoriutuminen eivät korreloi”. Nollahypoteesin vastinpari on vastahypoteesi, jonka mukaan asetettu nollahypoteesi ei pidä paikkaansa, mikä puolestaan yleensä on muotoa: “jotain on meneillään”. Se esimerkiksi tarkoittaisi että kissojen ja koirien painoissa on ero tai että älykkyys ja koulusuoriutuminen korreloivat. Datan perusteella lasketaan testisuure ja p-arvo, joka tarkoittaa todennäköisyyttä saada vähintään näin paljon nollahypoteesista poikkeava tulos olettaen että nollahypoteesi pitää paikkansa; toisin sanoen taustalla ollen pelkkää otantavirheen aiheuttamaa satunnaisuutta. Mikäli havaitaan matala p-arvo, hylätään nollahypoteesi, jolloin päätellään että vastahypoteesi saa tukea. Joko tapahtui epätodennäköinen tapahtuma, tai taustalla on muutakin kuin sattumaa.

Ongelma

Mikäli p-arvo ei ole merkitsevä (eli tyypillisimmin yli 0.05), vastahypoteesi ei saa riittävästi tukea, jolloin nollahypoteesi jää voimaan. Epäintuitiivisesti kuitenkin “Vastahypoteesi ei saa tukea” ei ole sama asia kuin “nollahypoteesi saa tukea”. Tämä on frekventistiseen tilastotieteeseen liittyvä keskeinen epäsymmetria: vain vastahypoteesi voi saada tukea. Nollahypoteesin paikkansapitävyys oletetaan p-arvon laskemisessa: sen pitävyyttä ei voida osoittaa ensin olettamalla että se pitää paikkansa. Tyypillisimmissä analyysiasetelmissa ei-merkitsevän p-arvon kanssa voidaan vain nostaa kädet ilmaan ja todeta että ei voida sanoa juuta tai jaata.

Tämä johtuu siitä että nollahypoteesin mukainen tulos voidaan saada useista syistä, joilla ei välttämättä ole tekemistä sen paikkansapitävyyden kanssa. Keskeisin näistä on vanha tuttavamme tilastollinen voima, joka tarkoittaa todennäköisyyttä saada merkitsevä tulos mikäli vastahypoteesi on tosi. Aiemman kirjoitukseni esimerkin mukaisesti: jos vertailemme useita kertoja kolmen kissan ja kolmen koiran keskimääräisiä painoja, saisimme hyvin harvoin merkitsevän tuloksen, vaikka tiedämme koirien olevan kissoja painavampia. Tämä johtuu siitä että testillä ei ole pienestä otoskoosta johtuen juurikaan voimaa löytää olemassaolevaakaan ilmiötä. Jos tilastollinen voima on matala, sanotaan 40%, saadaan 60%:ssa tutkimuksista nollatulos vaikka vastahypoteesi todellisuudessa pitäisi paikkansa. Ei tietenkään ole järkevää olettaa että heikkolaatuiset tutkimukset aidosti tukisivat nollahypoteesia useammin kuin laadukkaammat joissa havaintoja on enemmän.

Mikäli nollahypoteesi pitää paikkansa, on p-arvo tasajakutunut. Jos vastahypoteesi pitää paikkansa, se on jakaunut vasemmalle kallelleen, siten että pienet p-arvot ovat yleisempiä. Alla olevassa kuvassa tämä on havainnollisestettu simuloimalla 50000 kahden ryhmän vertailua ja piirtämällä jakaumat näiden p-arvoille. Vasemmalla ryhmien välillä ei ole mitään eroa, oikealla ryhmien arvot poimitaan jakaumista joilla on eri keskiarvot. Tämä on havainnollistus siitä mitä tilastollinen voima tarkoittaa käytännössä: mitä suurempi voima, sitä vahvemmin p-arvot pakkaantuvat vasemmalle. Kuitenkin huomattava osa oikeanpuoleisenkin kuvaajan p-arvoista on suuria vaikka ilmiön tiedetään olevan olemassa. Mitä heikompi tilastollinen voima, sitä paksumpi “jakauman häntä”.

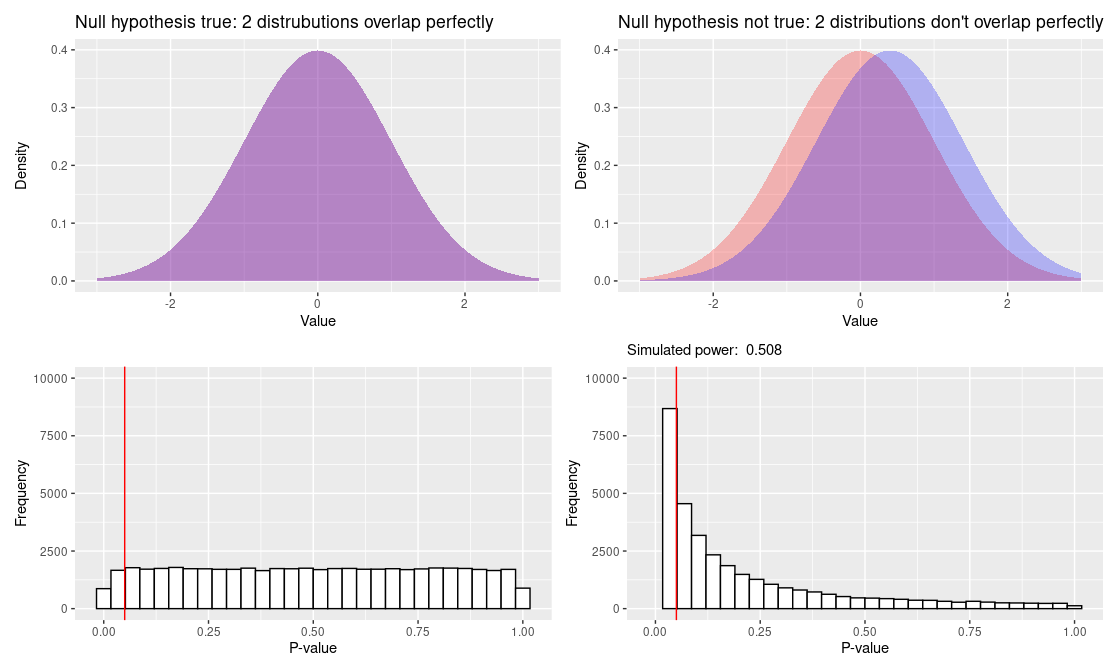
Koska heikosta tilastollisesta voimasta johtuen ei-merkiseviä tuloksia saadaan usein silloinkin kun vastahypoteesi on tosi, ei näiden oikea tulkinta voi olla “nollahypoteesi saa tukea”. Jos tällaiseen päättelyyn nojattaisiin, olisi nollahypoteesille tuen saaminen triviaalin helppoa, jolloin tällainen tuki ei olisi juuri minkään arvoista. Oleellisesti, tehtäisiin paljon ns tyypin 2 virheitä, koska tutkimus ei edes teoriassa tuottaisi usein merkitseviä tuloksia paikkansapitävälle vastahypoteesille. Tämä on keskeinen ongelma pienten otoskokojen tutkimuksissa, mikä takia nämä harvoin yksinään ovat juuri minkään arvoisia: vastahypoteesi voi saada tukea harvoin vaikka tutkittava ilmiö olisi olemassa, ja nollahypoteesin jääminen voimaan puolestaan ei kerro mitään.

Rautalangasta vääntäen: korkea p-arvo ei siis salli päätelmiä “ryhmien välillä EI OLE eroa” tai “muuttujien välillä EI OLE yhteyttä”. Monesti artikkeleissa tämä virhepäätelmä tehdään hienovaraisesti raportoimalla “the groups did not differ” tai “X was unrelated with Y”. Tällainen tulosten raportointi on muotoa evidence of absence vaikka oikea tulkinta on absence of evidence. Oikea tulkinta siis on että vastahypoteesille ei saatu tukea ottamatta kantaa nollahypoteesin paikkansapitävyyteen: “no evidence was found for group difference / relationship between X & Y”. Tämä on virhepäätelmänä hyvin yleinen, ja esiintyy jossain muodossaan sekä monissa uusia tuloksia raportoivissa artikkeleissa että alkuperäistutkimuksiin viittaavissa artikkeleissa.

Olemassaolemattomuuden osoittaminen: ekvivalenssitestaus

Jos nollahypoteesi ei voi saada tukea, herää kysymys: kuinka voidaan osoittaa että jotain ilmiötä ei ihan oikeasti ole olemassa? Ratkaisu näennäiseen ristiriitaan on, että nollahypoteesin ja ilmiön olemassaolemattomuuden ei tarvitse olla sama asia, vaikka näin useimmisten tehdään. Analyysi voidaan rakentaa vaihtoehtoisilla tavoilla, joihin lukeutuu keino löytää tukea 0-suuruista ilmiötä kohtaan. Alla olevassa kuvassa (mukaillen Harms & Lakens, 2018:aa) on esitelty neljä erilaista tapaa rakentaa testi, ja kukin on selitetty alla. Kuvassa vaaka-akseli kuvaa havaintun ryhmäeron suuruutta, ja nollahypoteesia sekä vastahypoteesia vastaavat alueet on merkitty.

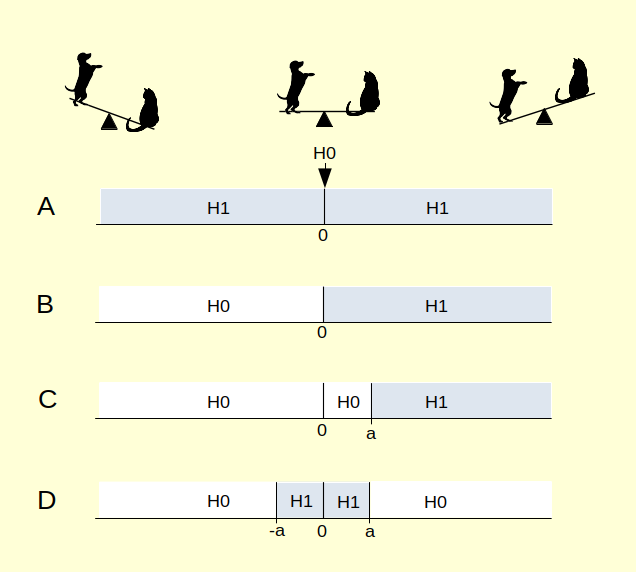
Tyypillisimmin nollahypoteesi vastaa tilannetta joissa ryhmien välinen ero tai kahden muuttujan yhteys on nolla (A). Tällöin mikä tahansa nollasta poikkeava tulos katsotaan vastahypoteesia tukevaksi, riippumatta sen koosta tai siitä, onko se positiivinen vai negatiivinen. Erityisesti suurilla aineistoilla voidaan saada hyvinkin merkitseviä tuloksia melko mitättömilläkin ilmiöillä.

Hypoteesitesti voidaan tehdä myös yksisuuntaisena (B), jolloin vain joko suuremmat tai pienemmät keskiarvoerot katsotaan vastahypoteesia tukevaksi, ja toista etumerkkiä olevat lasketaan nollahypoteesin piiriin. Esimerkiksi vastahypoteesia tukisi vain tulos että koirat ovat painavampia kuin kissat, mutta ei toisinpäin.

Lisäksi nollahypoteesiksi voidaan valita myös jokin muu luku kuin nolla. Tällöin voidaan testata onko ilmiön suuruus vähintään jokin etukäteen valittu minimiarvo a (C). Esimerkiksi ovatko koirat vähintään yli 2 kiloa kissoja painavampia. Yhdistämällä nämä kaksi asiaa: testin suunta, ja ilmiön suuruus jota vastaan testataan, voidaan rakentaa mielenkiintoisempia analyysejä.

Tätä kirjoitusta koskien kiinnostavin, ja tavanomaisesta poikkeavin on alin tilanne (D), jossa tyypillinen asetelma on käännetty päälaelleen. Tätä kutsutaan ekvivalenssitestaukseksi. Tässä nollan molemmin puolin on asetettu pienin kiinnostavan suuruinen ilmiö a, ja testataan asettuuko tulos virhemarginaaleineen näiden rajojen sisään. Vastahypoteesia (ei ilmiötä) tukee vain lähellä nollaa olevat tulokset virhemarginaalin ollessa riittävän kapea, ja nollahypoteesia (on ilmiö) kaikki muu. Tämä ei toki todista että ilmiön suuruus on tasantarkkaan 0, mutta mahdollistaa ilmiön suuruuden arvioinnin sen verran pieneksi että sen voi käytännössä katsoen ajatella olevan olematon.

Tämä menetelmä siis vaatii ilmiön suuruudelle jonkin raja-arvon asettamista, jota pienempää pidetään niin triviaaleja, että se on yhtä tyhjän kanssa (SESOI; smallest effect size of interest). Tämän jälkeen suoritetaan kaksi yksisuuntaista testiä: onko ilmiön suuruus samanaikaisesti pienempi kuin yläraja, ja suurempi kuin alaraja. Kun nollahypoteesiksi asetetaan vähintään tietyn suuruisen ilmiön olemassaolo, vastahypoteesille: “vähintään tämän suuruista ilmiötä ei ole”, on mahdollista saada tukea. Mikäli molemmat testit ovat merkitseviä, todetaan että poikkeama nollasta on enintään triviaalin suuruinen. Tällaisia analyysejä voi ajaa R:lla esimerkiksi TOSTER-paketilla.

Käytännössä analysointi voisi mennä esimerkiksi niin, että ensin testataan teorian tai olettamusten mukaista eroa joko perinteisellä yksi- tai kaksisuuntaisella testillä, ja mikäli tilastollisesti merkitsevää eroa ei havaita, katsotaan seuraavaksi ekvivalenssitestillä, saako ilmiön olemassaolemattomuus tukea. On toki mahdollista että tulos kiikkuu niin rajamailla että kummankaan puolesta ei saada näyttöä jolloin tulos on ns. inconclusive.

Ekvivalenssitestauksella voidaan saada tavanomaista ei-merkitsevää p-arvoa uskottavampaa tukea ilmiön olemassaolmattomuuden puolesta, sillä se vaatii että tuloksen virhemarginaali on melko tiukasti nollan ympärillä. Perinteisessä analyysissä ei-merkitsevä p-arvo puolestaan voidaan saada myös silloin kun virhemarginaali on niin että moni huomattavankin kokoinen ilmiö voisi teoriassa olla yhteensopiva tuloksen kanssa. Jos otoskoko on ekvivalenssitestauksessa liian pieni, virhemarginaali ylittää asetetut rajat jolloin testi ei puolla lähellä nollaa olevaa tulosta.

Loppusanat

Olen tässä kirjoituksessa havainnollistanut miksi ei-merkitsevästä p-arvosta ei voida sanoa että ilmiötä ei ole. Ei-merkitsevä tulos perinteisessä analyysissä voi seurata siitä että tutkimuksella ei ole riittävää tilastollista voimaa havaitakseen olemassaolevaa ilmiötä, jolloin virhemarginaali on niin suuri, että se sisältää monia nollasta kaukanakin olevia tuloksia. “Nollahypoteesi” perinteisessä mielessä ajateltuna ilmiön olemassaolemattomuutena voi saada tukea ainoastaan, mikäli testi on vartavasten suunniteltu testaamaan tätä: ekvivalenssitestauksen avulla. Menetelmä on ymmärtääkseni kohtuullisen uusi, enkä valitettavasti itse ole törmännyt siihen vielä yhdessäkään oppikirjassa.

Taustamateriaalia

Harms, C., & Lakens, D. (2018). Making “null effects” informative: Statistical techniques and inferential frameworks. Journal of Clinical and Translational Research. https://doi.org/10.18053/jctres.03.2017S2.007

Lakens, D., Scheel, A. M., & Isager, P. M. (2018). Equivalence Testing for Psychological Research: A Tutorial. Advances in Methods and Practices in Psychological Science, 1(2), 259–269. https://doi.org/10.1177/2515245918770963