Tilastollisesti merkitsevät ja ei-merkitsevät tulokset eivät automaattisesti ole ristiriidassa
It is possible that cumulative evidence across studies provides support for an effect, even when a more dichotomous evaluation of significant versus nonsignificant results suggests that the pattern of results is not very likely. This can happen because this heuristic, like all heuristics, ignores some information.
– Lakens & Etz, 2017
Lähes jokaisessa tutkimusartikkelissa vedetään yhteen aiempien tutkimusten tuloksia jostakin tietystä ilmiöstä. Usein tarkoituksena on katsoa, kuinka kuinka vahvasti nämä yhdessä tukevat johtopäätöstä ilmiön olemassaolosta. Yksittäisen tutkimuksen voi ajatella olevan nuoli, ja tarkoituksena on hahmottaa, kuinka vahvasti nuolten joukko yhdessä osoittaa tiettyyn suuntaan.
Tällaisen synteesin tekemiseen on olemassa lukuisia eri tapoja, niin laadullisia kuin määrällisiä. Valitettavan usein tutkimusten yhteenvetoon sovelletaan seuraavanlaista menetelmää: katsotaan kuinka monta tutkimusta on tehty ja lasketaan kuinka monessa tulos on ollut tilastollisesti merkitsevä (p-arvo alle .05) vs. ei-merkitsevä (p-arvo yli .05) ja tehdään johtopäätös näiden lukumäärien perusteella. Esimerkiksi artikkelin kirjallisuuskatsausosiossa saatetaan esitellä 10 tutkimusta joista vain 4:ssa on löytynyt jokin tilastollisesti mielenkiintoinen löydös; ero kahden ryhmän välillä tai yhteys kahdella muuttujalla. Kenties tulosten määrän perusteella otetaan kantaa että ilmiötä ei ehkä ole, tai että sen olemassaolo on kiistanalaista. Pahimmillaan tällainen päättely voi kuitenkin johtaa täysin harhaan (ks Kuva 2).
Tämä päättely vaikuttaa intuitiivisesti järkevältä: mitä suurempi on löydöksen ja “ei-löydöksen” tehneiden tutkimusten suhdeluku, sitä voimakkaampaa näyttö ilmiön puolesta tai sitä vastaan. Vaikka tämä järkeily ei ole täysin hakoteillä, on se silti karkea puolitotuus, jonka rajoitteellisuutta käsittelen tässä kirjoituksessa. Pelkästään merkitsevien tulosten laskemisen seurauksia voivat olla:
- tutkimusten laadun huomioimattomuus: liian suuri painoarvo heikkolaatuisille tutkimuksille, ja liian pieni painoarvo laadukkaille
- selityksiä tulosten erilaisuudelle sovitetaan satunnaiskohinaan
Tilastollinen merkitsevyys on käytännön ratkaisu
Kuvatussa päättelyssä ei-merkitsevien tulosten ajatellaan olevan ristiriidassa merkitsevien tulosten kanssa – siis osoittavan erilaiseen maailmantilaan. Kuitenkin merkitsevyys ja sen .05-raja ovat sopimuspohjaisia käytännön ratkaisuita, jotta yksittäisen analyysin kohdalla voitaisiin tehdä kategorinen päätös joko tuesta tai sen puutteesta. Tämä on kätevä tapa filtteröidä pois satunnaisvaihtelua, mutta yleistyy huonosti useampien tulosten arviointiin. Ajatellaan vaikka p-arvoja 0.04 ja 0.06: vaikka käytännön sopimuksella toinen lasketaan ilmiön olemassaoloa tukevaksi ja toinen ei niin luvut ja niitä vastaava data voivat olla hyvin lähellä toisiaan. Todellisuudessa tutkimusdata ei kategorisesti joko tue tai ole tukematta väitettä, vaan tukee sitä jollakin asteella (joka voi olla nolla tai negatiivinen). Kun tutkimusnäyttöä yhteenvetäessä katsoo vain merkitsevyyksiä, tapahtuu jotain samanlaista kuin jos matematiikan tehtävässä pyöristettäisiin karkeasti kaikki välivaiheet: lopputulos vääristyy. Ehkä tärkeämpänä, ei ole syytä olettaa että merkitseviä tuloksia saadaan aina, vaikka tutkittava ilmiö olisikin olemassa.
Otantavirhe
Tulosten merkitsevyys riippuu lukuisista seikoista: ilmiön olemassaolosta, sen voimakkuudesta (jos olemassa) sekä otantavirheen ja mittausvirheen suuruudesta. Täysin samanlaisina toteutettujen tutkimustenkaan tulokset eivät koskaan ole identtisiä otantavirheen takia. Sillä tarkoitetaan tulosten heittelehtimistä sen mukaan, ketkä koehenkilöt tai havainnot on satuttu poimimaan otokseen. Esimerkiksi koirat ovat keskimäärin painavampia kuin kissat. Jos molemmista ottaisi satunnaisotoksen, useimmiten niissä myös havainnollistuisi tämä ero. Kuitenkin välillä mukaan saattaa sattumalta päätyä vain niin pieniä koiria ja niin isoja kissoja, että eroa ei havaita. Näin voi käydä etenkin silloin, jos otoskoko on erityisen pieni, esimerkiksi vain kolme kissaa ja kolme koiraa.
Tilastollinen voima
Tilastollisella voimalla tarkoitetaan todennäköisyyttä saada tilastollisesti merkitsevä tulos, mikäli todellisuudessa tutkittava eroavaisuus tai yhteys on olemassa. Edeltävässä kissojen ja koirien painoja vertailevassa esimerkissä voima on äärimmäisen heikko, sillä pienessä aineistossa ero painoissa voi olla olematon tai jopa päinvastainen maailmantilaan nähden. Heikon voiman takia tällaisissa painotutkimuksissa saataisiin hyvin usein tuloksia jotka ovat “ristiriidassa” vakiintuneen totuuden kanssa jos katsotaan vain tilastollista merkitsevyyttä.
Voiman määrittävät otoskoko sekä ilmiön suuruus (efektikoko), joka tässä kuvaisi sitä, kuinka paljon kissoja painavampia koirat ovat. Otoskoon kasvattaminen pienentää otantavirhettä, jolloin heikommatkin ilmiöt voidaan havaita luotettavasti. Esimerkiksi 80% suuruinen tilastollinen voima tarkoittaa, että jos ilmiö on vähintään näin vahva niin tarvitaan vähintään näin suuri otos, jotta ero havaittaisiin ainakin 80%:ssa tätä otoskokoa käyttävissä identtisissä tutkimuksia. Mikäli voima jää matalaksi, ei todellistakaan ilmiötä löydetä luotettavasti otantavirheen heiluttaessa tuloksia, ja koko analyysin mielekkyys on kyseenalainen. Alla olevassa kuvassa on havainnollistettu simulaatiolla kuinka tilastollinen voima käyttäytyy otoskokoa kasvattaessa: p-arvot pakkautuvat vasemmalle, mutta hiljalleen.
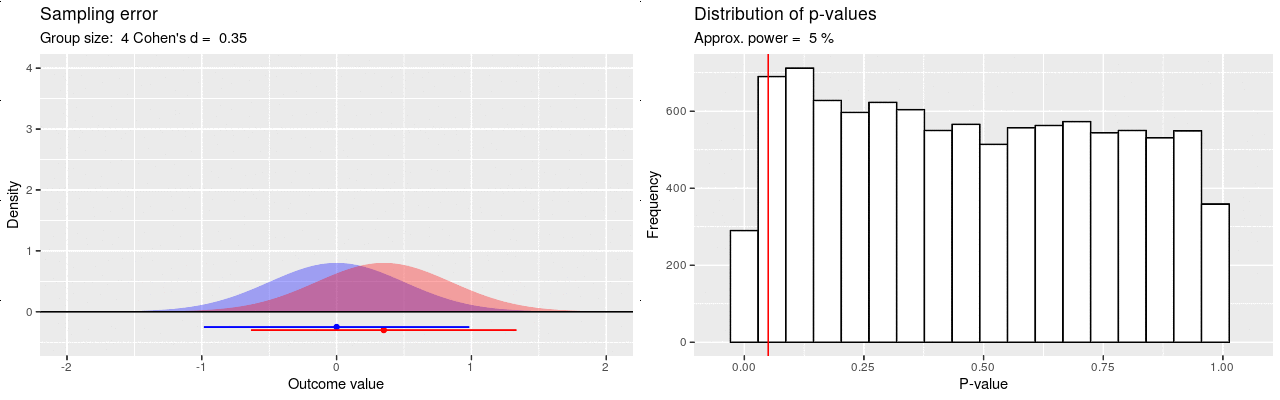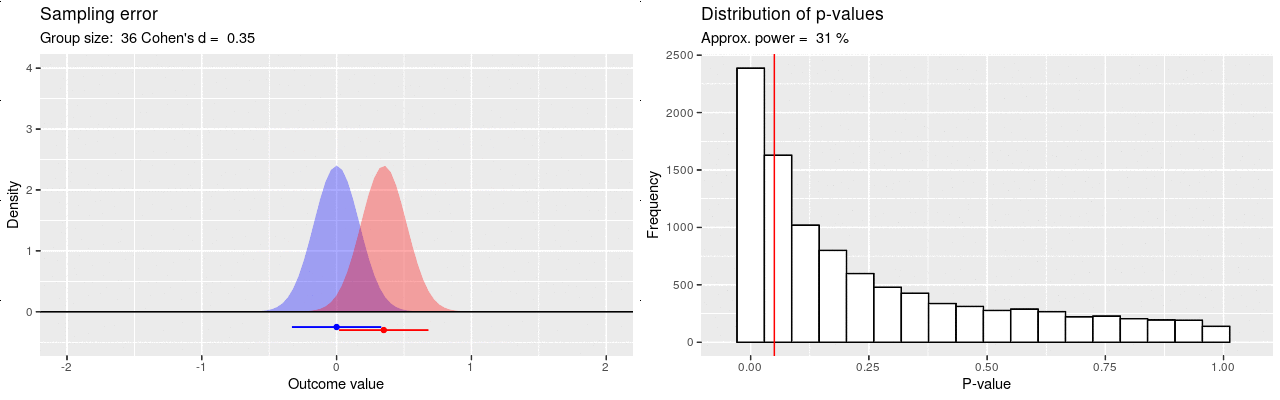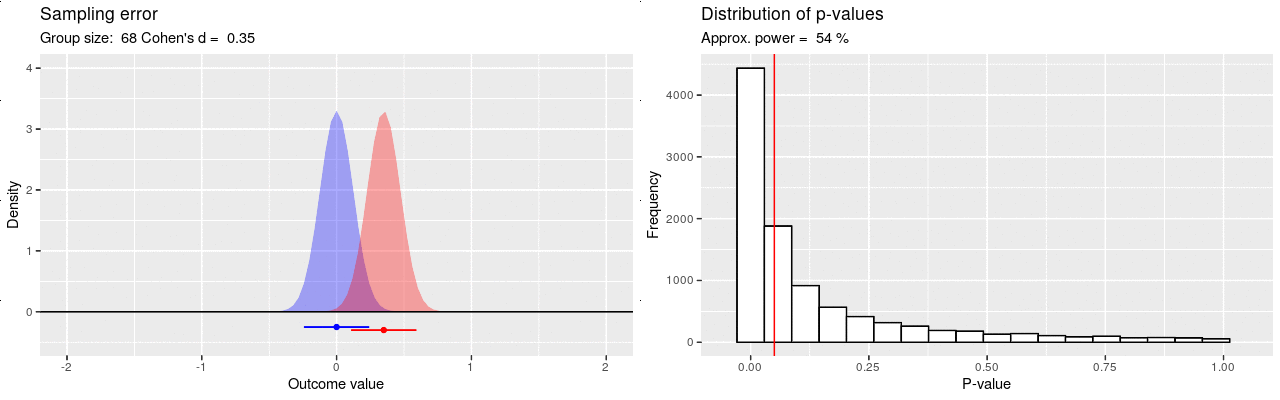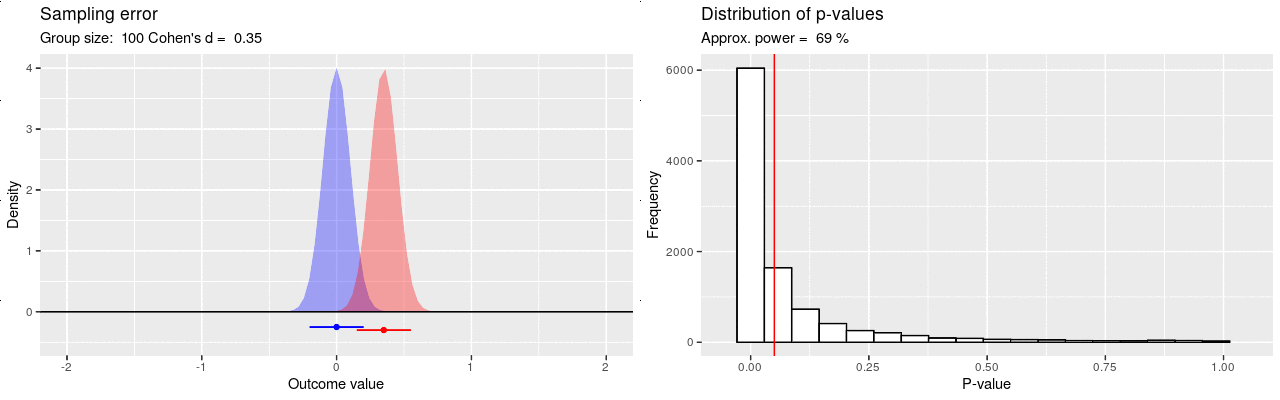
Ollakseen informatiivinen, tutkimuksella tulisi olla kohtalaisen hyvä todennäköisyys / voima (esim 80%) pystyä havaitsemaan hypoteesin mukainen ilmiö. Sama tutkimus voi olla riittävä havaitakseen luotettavasti vahvan ilmiön, mutta riittämätön havaitakseen vaimean. Mikäli tutkitaan vaimeita ilmiöitä, tarvitaan enemmän dataa kuin vahvojen ilmiöiden tutkimiseen. Kun suunnitellaan uutta tutkimusta, modernin ohjeistuksen mukaan otoskoko pitäisi määrittää niin, että saavutetaan hyvä tilastollinen voima huomioiden ilmiön oletettu suuruusluokka. Usein ilmiön suuruutta ei tiedetä etukäteen, joten otoskoon määrittämistä varten joudutaan tekemään sivistynyt arvaus sen suuruusluokasta. Siis: “Jos oletamme kissojen ja koirien painoeron olevan näin suuri, tarvitsisimme näin monta kissaa ja koiraa havaitaksemme tilastollisesti merkitsevän eron 80%:ssa tätä otoskokoa käyttävissä identtisissä tutkimuksissa.” Kuitenkin jopa näin korkealla voimalla viidesosa tutkimuksista ei havaitse todellista ilmiötä, vaan tulokset saattavat jäädä killumaan enemmän tai vähemmän merkitsevyysrajan yläpuolelle.
“Voitaisiin ajatella, ettei efektin tarvitse löytyä joka kerta - riittää, kunhan suurin osa tutkimuksista on merkitseviä.” Tällainen ajattelu ei kuitenkaan toimi, mikäli valtaosa tutkimuksista on otoskooltaan pieniä suhteessa ilmiöön. Tilastollinen voima voi pahimmillaan olla vain parinkymmenen prosentin luokkaa, jolloin ainoastaan viidesosa tutkimuksista havaitsisi olemassaolevan ilmiön. Varsin usein psykologiassa tilanne on ollut tämänsuuntainen pienten tutkimusten dominoidessa erityisesti kokeellista tutkimusta (Szucs & Ionnadis, 2017); ne eivät ole riittävän isoja voidakseen luotettavasti löytää psykologiassa tyypillisen suuruisia ilmiöitä.
Voimajakauma
Kun ymmärtää, kuinka otantavirhe heiluttaa tuloksia yksittäisissä tutkimuksissa, voi alkaa hahmottamaan, kuinka tulokset käyttäytyvät, kun tutkimuksia on useita.
Voidaan ajatella, että usean tutkimuksen joukolla on jakauma tilastollista voimaa. Yhdessä tutkimuksessa kissoja ja koiria voi olla kumpiakin 5, toisessa 8, kolmannessa 15, neljännessä 25 ja viidennessä 50. Sanotaan, että vastaavat tilastolliset voimat ovat 20%, 25%, 40%, 60% ja 80%. Todennäköisyyslaskennan taitajat osaavat nyt selvittää, kuinka todennäköistä on, että saadaan 1, 2, 3 jne ei-merkitsevää tulosta, vaikka painoeron tiedetään olevan olemassa. Mitä pienempi keskimääräinen tilastollinen voima, sitä enemmän nollatuloksia tulee olemassaolevistakin ilmiöistä.
Niin kauan kun tilastollinen voima pysyy selkeästi alle 100%:ssa, osa tutkimuksista tulee tuottamaan nollatuloksen ennen pitkää, vaikka hypoteesi pitäisikin paikkansa. 100% tilastollinen voima ei edes tyypillisesti ole tutkijoiden käytössä olevia resursseja ajatellen realistinen tavoite, minkä takia ongelma on sisäänrakennettuna merkitsevyyttä korostavaan ajatteluun.
Efektikoko ei aina ole pelastus
Tilastollisesti sivistynyttä lukijaa on koulutettu katsomaan myös esimerkiksi efektikokoa. Siinä missä p-arvo kuvaa datan epätodennäköisyyttä oletuksella että ilmiötä ei ole, efektikoko on otokseen pohjautuva arvio sen voimakkuudesta. Kuitenkin p-arvo ja efektikoko ovat tiiviisti matemaattisesti kytköksissä, ja usein toinen voidaan liki ykiselitteisesti laskea toisen avulla jos otoskoko ja käytetty testisuure tiedetään. Itse asiassa tietyllä otoskoolla tarvitaan vähintään tietynsuuruinen havaittu efektikoko, jotta tulos voi olla tilastollisesti merkitsevä. Siten maagista p-arvon 0.05 rajaa vastaa jokin efektikoko, jota pienemmät havaitut efektikoot eivät yksinkertaisesti voi tuottaa merkitseviä tuloksia tietyllä otoskoolla. Vaikka efektikoko onkin tulkinnallisesti mielekkäämpi luku kuin p-arvo, sen suuruus voi heittelehtiä otoskoon funktiona aivan yhtä villisti kuin tilastollinen merkitsevyys.
Seurauksena pienten otosten tutkimukset usein yliarvioivat efektikokoa. Koska 5% tutkimuksista tuottaa sattumalta merkitseviä tuloksia kun ilmiötä ei ole, näitä vastaavat efektikoot ovat VALTAVIA pienten otosten tapauksessa. Siten ei voida suoraan sanoa että suuren efektikoon tutkimukset olisivat automaattisesti vakuuttavampia ilmiön olemassaolosta. Eräs replikaatiokriisin “pienempi muoto” onkin ollut havainto, että toistotutkimukset suurilla otoskooilla ovat tuottaneet systemaattisesti huomattavasti pienempiä efektikokoja verrattuna alkuperäistutkimuksiin (Open Science Collaboration 2015).
Meta-analyyttinen ajattelu
Herää kysymys: jos matalan tilastollisen voiman tutkimukset voivat antaa näin ailahtelevan kuvan todellisuudesta, mikä on niiden arvo? Vastaus on: ei juuri mikään, mikäli katsotaan pelkästään tilastollista merkitsevyyttä.
Palataan esimerkkiin kolmesta otokseen poimitusta kissasta ja koirasta. Tällainen “tutkimus” on ilmiselvästi liki arvoton, jos haluaisimme vertailla eläinten painoja, koska sillä ei kovin luotettavasti voitaisi todeta olemassaolevia eroja. Käytetty data itsessään ei kuitenkaan ole arvotonta, vaan sisältää pienen määrän informaatiota ilmiöstä. Jos olisi tehty kymmenen tällaista minitutkimusta, datat yhdistämällä saataisiin vertailu, joka sisältää 30 kissaa ja 30 koiraa. Tällöin on jo olemassa paremmat edellytykset havaita todellinen ilmiö.
Tämä on järkeily meta-analyysissa, missä tulokset useasta tutkimuksesta yhdistetään numeerisesti. Meta-analyysissä pyritään yksittäisten tutkimusten tuloksia yhdistämällä vastaamaan samoihin kysymyksiin kuin yksittäisessä tutkimuksissa: onko ilmiötä olemassa, ja kuinka voimakas se on. Meta-analyysi toimii garbage in, garbage out -periaatteella, eli sen tulos lähestyy todellista maailmantilaa vain mikäli tutkimusten joukko on harhaton, mikä voi usein olla epärealistinen oletus.
Kyse ei kuitenkaan ole vain kirjaimellisesti meta-analyysin tekemisestä, vaan tietynlaisesta tavasta suhtautua yksittäisiin tutkimuksiin. En ole ehdottamassa, että jokaisen tutkimusongelman suhteen tulisi tehdä meta-analyysi aina kun halutaan vetää yhteen tutkimusnäyttöä. Sen sijaan ehdotan että merkitsevyyskeskeisestä ajattelusta siirrytään meta-analyyttiseen ajatteluun, jossa jokainen yksittäinen tutkimus ajatellaan osana kuvitteellista meta-analyyttistä “megadataa”, joka koostuu sekä jo olemassaolevista tutkimuksista että toistaiseksi suorittamattomista tutkimuksista.
Merkitsevyyskeskeisessä ajattelussa toisiaan hyvin lähellä, mutta merkitsevyysrajan eri puolilla olevien p-arvojen 0.04 ja 0.06 ajatellaan osoittavan vastakkaisiin suuntiin: toinen tukee ilmiön olemassaoloa, toinen ei. Meta-analyyttisessä ajattelussa puolestaan molemmat yhdessä ja muiden tutkimusten kanssa voivat osoittaa ilmön olemassaoloon tai olemattomuuteen. Kenties myöhemmät tutkimukset tuottavat vastaavanlaisia tuloksia (sekä suuruusluokaltaan että p-arvoiltaan), tai ehkä nämä molemmat olivat sattumalta poikkeuksellisen epätodennäköisiä.
Alla olevassa kuvassa on simuloitu 40 kahden ryhmän vertailua olemassaolevalla ryhmäerolla, jaettuna neljälle tilastollisen voiman tasolle. Yläoikeassa paneelissa ero ajattelutavoissa nähdään selvimmiten: paperilla kuulostaa heikolta että 2/10 tutkimuksesta löysi eron, mutta kuvasta nähdään että yhdessä kymmenen tutkimusta tukee sen olemassaoloa.
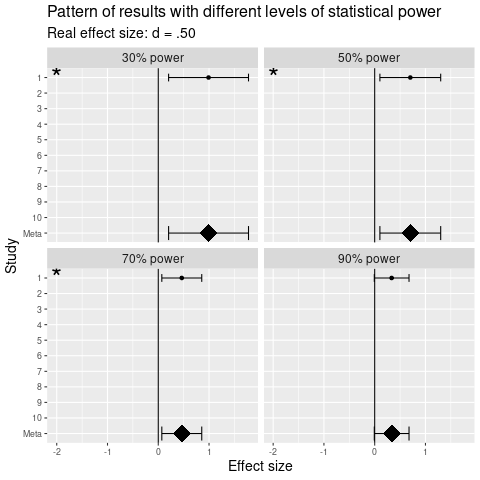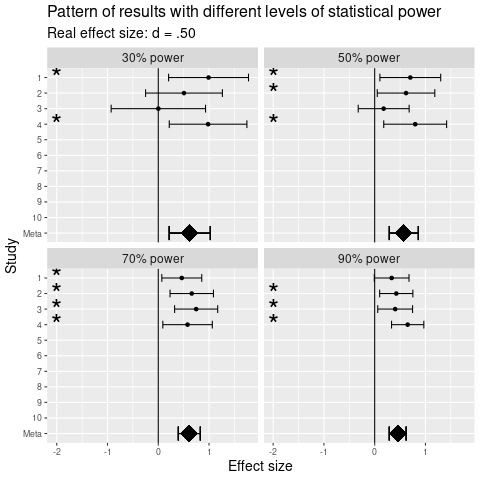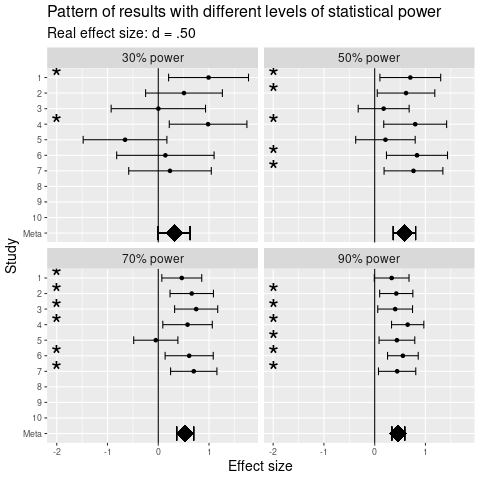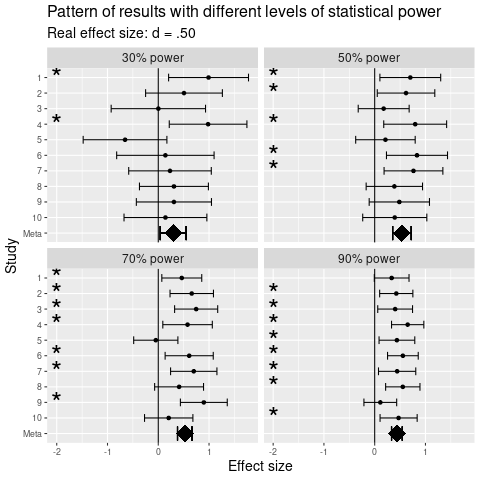
Konkreettisesti ero ajattelutavoissa näkyy siinä, kuinka suhtautua, kun artikkelissa kerrotaan että osa tutkimuksista (joko artikkelissa raportoiduista tai taustakirjallisuudessa olevista) on havainnut viitteitä ilmiöstä, mutta osa ei. Merkitsevyyskeskeisessä ajattelussa näille erilaisille tuloksille haetaan selityksiä esimerkiksi eroavista metodologioista tai tilannetekijöistä. Meta-anayyttistä ajattelua on todeta tähän, että eräs todennäköinen syy on otantavirheen ja tilastollisen voiman aiheuttama vaihtelu, joten tällaisia päätelmät jäävät spekulaation asteelle. Varomaton merkitsevyyskeskeinen ajattelu voi jopa johtaa virheellisiin teoreettisiin päätelmiin, mikäli teoriaa sovitetaan brutaalisti merkitsevien ja ei-merkitsevien tulosten ympärille.
Loppusanat
Tässä kirjoituksessa olen koittanut avata minkälaisiin virhepäätelmiin voidaan sortua, mikäli tuloksia useista tutkimuksista vedetään yhteen katsoen tilastollista merkitsevyyttä. Keskeisesti, vaikka ilmiö olisikin olemassa, on erittäin odotettavissa että ei-merkitseviä tuloksia tulee joskus. Niiden määrään vaikuttaa tutkimusten tilastollinen voima: mitä enemmän tutkimuksia, joissa on matala voima, sitä enemmän ei-merkitseviä tuloksia tulee otantavirheen takia. Selityksiä eroille tulosten merkitsevyydessa saatetaan hakea eroista metodologiassa, mutta vaikka tämä onkin mahdollista, voi yksinkertaisempi selitys olla usein tilastollinen voima.
Acknowledgements
Kiitos Piia Turuselle tämän kirjoituksen draftin kommentoinnista.
Viitteet:
Lakens, D., & Etz, A. J. (2017). Too True to be Bad: When Sets of Studies With Significant and Nonsignificant Findings Are Probably True. Social Psychological and Personality Science, 8(8), 875–881. https://doi.org/10.1177/1948550617693058
Open Science Collaboration. (2015). Estimating the reproducibility of psychological science. Science, 349(6251), aac4716–aac4716. https://doi.org/10.1126/science.aac4716
Szucs, D., & Ioannidis, J. P. A. (2017). Empirical assessment of published effect sizes and power in the recent cognitive neuroscience and psychology literature. PLOS Biology, 15(3), e2000797. https://doi.org/10.1371/journal.pbio.2000797